Semantic Temporal Perception:Semantic processing and statistical learning of 'yihou' in Mandarin Chinese | Discussion(preliminary)
experiment page | forum posts | presentation handout | PAPER FOR SEMANTICS II | abstract
[guling.semantics2]
corpus consulted: corpus query interface
Sharoff, S. (2006) Creating general-purpose corpora using automated search engine queries. In Marco Baroni and Silvia Bernardini, editors, WaCk y! Working papers on the Web as Corpus. Gedit, Bologna. PDF
Sharoff, S. (2006) Creating general-purpose corpora using automated search engine queries. In Marco Baroni and Silvia Bernardini, editors, WaCk y! Working papers on the Web as Corpus. Gedit, Bologna. PDF
histogram of meaning type frequencies
Coding of target words in the histogram
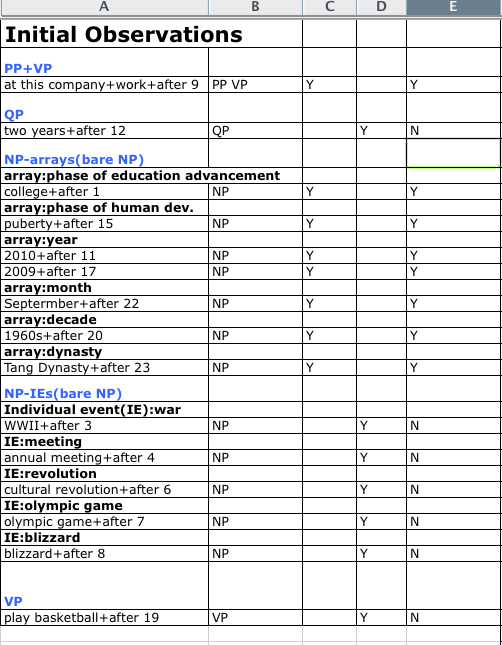
at this company+work+after 9; college+after 1; 2010+after 11;3rd movement+after 14;puberty+after 15;
development+after 16 ; 2009+after 17 ; seventh war+after 18 ; play basketball+after 19 ; 1960s+after 20 ;
Septermber+after 22 ; Tang Dynasty+after 23 ; two years+after 12 ; WWII+after 3 ; annual meeting+after 4 ;
cultural revolution+after 6 ; olympic games+after 7 ; blizzard+after 8 ;
development+after 16 ; 2009+after 17 ; seventh war+after 18 ; play basketball+after 19 ; 1960s+after 20 ;
Septermber+after 22 ; Tang Dynasty+after 23 ; two years+after 12 ; WWII+after 3 ; annual meeting+after 4 ;
cultural revolution+after 6 ; olympic games+after 7 ; blizzard+after 8 ;
[Contents]
I Data and First Approximation
1. The varied temporal interpretation of non-bare and bare NP+yihou in different context
2. The syntactic distribution of meaning of XP+yihou
3. First approximation to the problem: Bare NP+yihou, phase in an array, and IE(PHIE Hypothesis)
4. Two hypotheses about the meaning of bare NP+yihou: (see below)
a. categorical
b. gradient (statistical)
II Experiment Design
1.test question structure
2.novel array tests
3.novel array tests on high frequency IE items
III Results and Discussion
1.Preliminary results and the 2 hypotheses
2.Statistical modeling
3.Discussion
1. The varied temporal interpretation of non-bare and bare NP+yihou in different context
2. The syntactic distribution of meaning of XP+yihou
3. First approximation to the problem: Bare NP+yihou, phase in an array, and IE(PHIE Hypothesis)
4. Two hypotheses about the meaning of bare NP+yihou: (see below)
a. categorical
b. gradient (statistical)
II Experiment Design
1.test question structure
2.novel array tests
3.novel array tests on high frequency IE items
III Results and Discussion
1.Preliminary results and the 2 hypotheses
2.Statistical modeling
3.Discussion
Introduction
Overall, this project is about cognitive information processing in semantic processing in context deprived sentences. For some linguistic structures, their meaning depend on context specific information for clear interpretation. When the context is null, however, they can be interpreted ambiguously. The English word 'after', for instance, is not such a case, because no matter what contexts are present or absent, it has a consistent, categorical interpretation: after the end of a duration (e.g., after 2010 means after the end of 2010).
In contrast, the Chinese 'yihou' (meaning after) is a case where in the combination of [NP+yihou], when there is no clear context indication of whether it means after the beginning or the end of the duration, it can be ambiguous. However, that doesn't mean it has no systematic semantic interpretation when context independent. This is the research question of this paper: what rules govern the interpretation of context deprived bare NP+yihou combinations? I will show that in this case, it is not categorical but a probabilistic/gradient phenomenon. In this case, I propose that the interpretation of temporal meanings of yihou probabilistically depends on:(1) implicit semantic categories of phase of an array, and (2) statistic learning of linguistic input.
This paper also draws on the research on the systematic organization of gradient phenomena vs. categorical phenomena. In linguistics, theoretically, we used to deal only with categorical phenomena. A syntactic entity belongs to this category or that category. It's not part of the assumption that it belongs to this category 80% of the time and the other 20% of the time. This is the assumption by the generative grammar, where only categorical representation exists in the memory storage, and is later transformed according to a series of transformational rules and generates the surface form. However, recent cognitive science research has revealed strong evidence for statistical frequency based processing (not only in the language domain) and the exemplar based storage (exemplar theory). In this performance based model (instead of a competence based model), details of the usage (especially high frequency items) are stored in the brain. In early childhood learning, only these exemplars from environmental input are stored. These exemplars may differ from each other in gradient details, but more importantly their similarity will emerge later as a category. Therefore, details of the gradient linguistic phenomena are already stored in the brain alongside the categories, and they are not generated from mere abstract categories stored in the brain with no instances of usage of concrete exemplars are available. The exemplar model has evidence of support from a wide domain of linguistic research , such as phonology, syntax, pragmatics, L2 learning, etc. The usage-frequency based model is especially suitable for dealing with gradient and probabilistic phenomena. In contrast to generative grammar, which claims that all gradience come from random variation in human biology, the statistical models find quantitative patterns in the gradient phenomena and have the predicative power of predicting the statistical distributional patterns of the observed frequency in a given phenomenon. This project attempts to do exactly that.
In contrast, the Chinese 'yihou' (meaning after) is a case where in the combination of [NP+yihou], when there is no clear context indication of whether it means after the beginning or the end of the duration, it can be ambiguous. However, that doesn't mean it has no systematic semantic interpretation when context independent. This is the research question of this paper: what rules govern the interpretation of context deprived bare NP+yihou combinations? I will show that in this case, it is not categorical but a probabilistic/gradient phenomenon. In this case, I propose that the interpretation of temporal meanings of yihou probabilistically depends on:(1) implicit semantic categories of phase of an array, and (2) statistic learning of linguistic input.
This paper also draws on the research on the systematic organization of gradient phenomena vs. categorical phenomena. In linguistics, theoretically, we used to deal only with categorical phenomena. A syntactic entity belongs to this category or that category. It's not part of the assumption that it belongs to this category 80% of the time and the other 20% of the time. This is the assumption by the generative grammar, where only categorical representation exists in the memory storage, and is later transformed according to a series of transformational rules and generates the surface form. However, recent cognitive science research has revealed strong evidence for statistical frequency based processing (not only in the language domain) and the exemplar based storage (exemplar theory). In this performance based model (instead of a competence based model), details of the usage (especially high frequency items) are stored in the brain. In early childhood learning, only these exemplars from environmental input are stored. These exemplars may differ from each other in gradient details, but more importantly their similarity will emerge later as a category. Therefore, details of the gradient linguistic phenomena are already stored in the brain alongside the categories, and they are not generated from mere abstract categories stored in the brain with no instances of usage of concrete exemplars are available. The exemplar model has evidence of support from a wide domain of linguistic research , such as phonology, syntax, pragmatics, L2 learning, etc. The usage-frequency based model is especially suitable for dealing with gradient and probabilistic phenomena. In contrast to generative grammar, which claims that all gradience come from random variation in human biology, the statistical models find quantitative patterns in the gradient phenomena and have the predicative power of predicting the statistical distributional patterns of the observed frequency in a given phenomenon. This project attempts to do exactly that.
Data
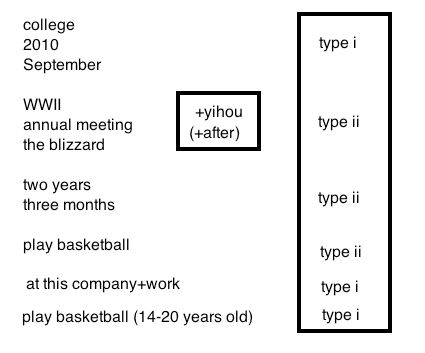
This project investigates the curious temporal meaning of 'yihou' (after) in MC. As a first characterization, MC 'yihou' could mean after the beginning of a duration (e.g., college), or the end. This is in sharp contrast to English, which is always the end. We will refer to the beginning as type i meaning, and end as type ii. Therefore, MC 'yihou' can be either type i or type ii, but English 'after' is always type ii. A first attempt is to establish a meaning type as it is related to the syntactic categories. While some distribution patterns emerge in the following data across syntactic categories, they seem to be consistent. It is within the same syntactic category (i.e., NPs) that the interpretation is ambiguous and is most interesting. Therefore, the ambiguity of 'yihou' is not due to syntactic differences.
Mandarin Chinese: (probabilistic)
(1)a non-bare NP(NP embedded in VP): V+NP, type i meaning (phase)
tamen shi shang daxue yihou renshi de.
they BE enter college after meet PART
"they met after they entered college".
(1)b bare NP: contextually contrast use, type ii meaning
youyu qianyizhen chuchai, mei neng jishi jiang ziji daxue ji daxue yihou de shiqing xie xialai
because recently travel, not can in time PARTself [college and college after] things write down
"Because I have been traveling a lot lately, I have not had time to write down things about my life in college and after college".
(2)bare NP: type i meaning (phase)
tamen shi daxue yihou renshi de.
they BE [college after] meet PART
"they met after college".
(3)non-bare NP(actually a VP): V+NP, type i meaning (phase?individual event?)
tamen shi jinru erzhan yihou renshi de.
they BE enter WWII after meet PART
"they met after the beginning of WWII".
(4)bare NP:type ii meaning (phase?IE?)
tamen shi erzhan yihou renshi de.
they BE [WWII after] meet PART.
"they met after WWII".
(5)bare NP:type ii meaning(not a phase)
tamen shi jinnian nianhui yihou renshi de.
they BE this year [anunual meeting after] meet PART
"they met after this year's annual meeting".
(6)VP:type ii meaning
ta da lanqiu yihou wo lai le.
he [play basketball after] I came PART
"I came after he played basketball".
From examples (1)-(6) we see that:
a. the interpretation of yihou has different distributions across NPs, and other syntactic categories.
b. within NPs, it can be either type i or type ii.
c. the distribution is not random: type i meaning is associated with interpreting a duration as a phase in an array.
Consider this in contrast to English data:
ENGLISH: (categorical type ii meaning)
(8) They met after they entered college.
(9) During college, they did not know each other; after college, they finally met.
(10)They met [after college].
(11)They met [after WWII].
For English data we see a categorical phenomenon: no matter what kind of context may appear in a particular frequency in real speech, the meaning of 'after' is always categorical : a type ii meaning.
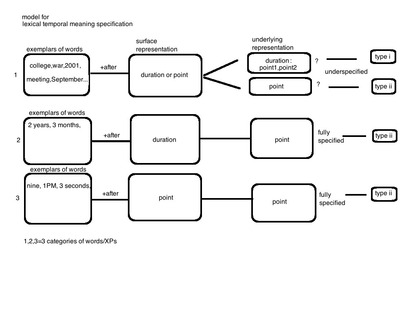
The initial results from these examples are summarized in the table below (left). Basically a phase in an array is associated with type i meaning, for a bare NP+yihou. Here, I give a definition of the 'phase in an array' in predicate logic:
[Phase in an array]
x is a phase in an array if x is a member of the set: {F | x1,x2,x3,...xn} where F represents a feature that is present in all members of the set. Instances of F may be year, month, phase of human development, phase of school, etc. In addition, the member of the array set must satisfies these conditions:
(1)they are ordered in a temporal ascending order;
(2)each element of the array is considered as an interval rather than a point by speakers;
(3)there is no time t in between xn and xn+1 where an element xm at t is not a member of the array (this condition is hypothetical);
Mandarin Chinese: (probabilistic)
(1)a non-bare NP(NP embedded in VP): V+NP, type i meaning (phase)
tamen shi shang daxue yihou renshi de.
they BE enter college after meet PART
"they met after they entered college".
(1)b bare NP: contextually contrast use, type ii meaning
youyu qianyizhen chuchai, mei neng jishi jiang ziji daxue ji daxue yihou de shiqing xie xialai
because recently travel, not can in time PARTself [college and college after] things write down
"Because I have been traveling a lot lately, I have not had time to write down things about my life in college and after college".
(2)bare NP: type i meaning (phase)
tamen shi daxue yihou renshi de.
they BE [college after] meet PART
"they met after college".
(3)non-bare NP(actually a VP): V+NP, type i meaning (phase?individual event?)
tamen shi jinru erzhan yihou renshi de.
they BE enter WWII after meet PART
"they met after the beginning of WWII".
(4)bare NP:type ii meaning (phase?IE?)
tamen shi erzhan yihou renshi de.
they BE [WWII after] meet PART.
"they met after WWII".
(5)bare NP:type ii meaning(not a phase)
tamen shi jinnian nianhui yihou renshi de.
they BE this year [anunual meeting after] meet PART
"they met after this year's annual meeting".
(6)VP:type ii meaning
ta da lanqiu yihou wo lai le.
he [play basketball after] I came PART
"I came after he played basketball".
From examples (1)-(6) we see that:
a. the interpretation of yihou has different distributions across NPs, and other syntactic categories.
b. within NPs, it can be either type i or type ii.
c. the distribution is not random: type i meaning is associated with interpreting a duration as a phase in an array.
Consider this in contrast to English data:
ENGLISH: (categorical type ii meaning)
(8) They met after they entered college.
(9) During college, they did not know each other; after college, they finally met.
(10)They met [after college].
(11)They met [after WWII].
For English data we see a categorical phenomenon: no matter what kind of context may appear in a particular frequency in real speech, the meaning of 'after' is always categorical : a type ii meaning.
The initial results from these examples are summarized in the table below (left). Basically a phase in an array is associated with type i meaning, for a bare NP+yihou. Here, I give a definition of the 'phase in an array' in predicate logic:
[Phase in an array]
x is a phase in an array if x is a member of the set: {F | x1,x2,x3,...xn} where F represents a feature that is present in all members of the set. Instances of F may be year, month, phase of human development, phase of school, etc. In addition, the member of the array set must satisfies these conditions:
(1)they are ordered in a temporal ascending order;
(2)each element of the array is considered as an interval rather than a point by speakers;
(3)there is no time t in between xn and xn+1 where an element xm at t is not a member of the array (this condition is hypothetical);
Experiment Design
Hypothesis 1: bare NPs have categorical interpretation when combined with 'yihou' (after): if it is a phase in an array,it is interpreted as the beginning; if it is not, in other words, considered an individual event (even though underlyingly it is a duration), it is interpreted as the end.
In order to test this hypothesis (derived from the initial observation above), I designed semantic judgement experiment that involves phase in an array, IE, and novel arrays that are normally interpreted as IEs. Two important questions I bare in mind while designing the experiment questions are:
(1) Are array effects consistently and categorically observed as type i meaning?
(2) If a target word is normally interpreted as type ii meaning, can it be interpreted as type i meaning when experimentally manipulated into an array context?
(3) If a target word is novel (i.e., with no pre-existing strong inclination to type i or type ii), can I manipulate it into type i meaning, given the right context?
Things to keep in mind in experimental design:
1. use sentences with minimum context info (as context could block one interpretation or the other), and consistent format
Questions are of the format given in the previous section examples:
=====================================================
Test Question format:
(a)tamen hi ____ yihou renshi de.
they BE____ after meet PART
"They met after ___".
What is the earliest time they could have known each other?
A. sophomore year in college
B. one year after graduation from college
C. two years after graduation from college
=====================================================
2. use of distraction sentences "yiqian" (before)
3. use of novel arrays (example: phases in a sonata form and symphony)
4. use of contextually manipulated arrays (example: war: WWII vs. the seventh war in a series of 12 wars)
5. future: time break between phases (war vs. olympic games)
11 subjects across ages (20s-50s) who are native speakers of Mandarin participated in the experiment.
In order to test this hypothesis (derived from the initial observation above), I designed semantic judgement experiment that involves phase in an array, IE, and novel arrays that are normally interpreted as IEs. Two important questions I bare in mind while designing the experiment questions are:
(1) Are array effects consistently and categorically observed as type i meaning?
(2) If a target word is normally interpreted as type ii meaning, can it be interpreted as type i meaning when experimentally manipulated into an array context?
(3) If a target word is novel (i.e., with no pre-existing strong inclination to type i or type ii), can I manipulate it into type i meaning, given the right context?
Things to keep in mind in experimental design:
1. use sentences with minimum context info (as context could block one interpretation or the other), and consistent format
Questions are of the format given in the previous section examples:
=====================================================
Test Question format:
(a)tamen hi ____ yihou renshi de.
they BE____ after meet PART
"They met after ___".
What is the earliest time they could have known each other?
A. sophomore year in college
B. one year after graduation from college
C. two years after graduation from college
=====================================================
2. use of distraction sentences "yiqian" (before)
3. use of novel arrays (example: phases in a sonata form and symphony)
4. use of contextually manipulated arrays (example: war: WWII vs. the seventh war in a series of 12 wars)
5. future: time break between phases (war vs. olympic games)
11 subjects across ages (20s-50s) who are native speakers of Mandarin participated in the experiment.
Preliminary Discussion based on results
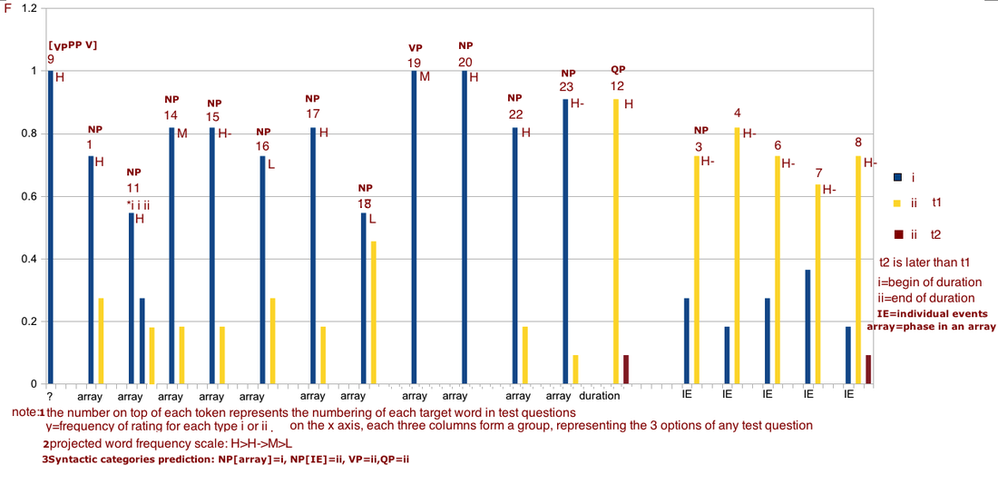
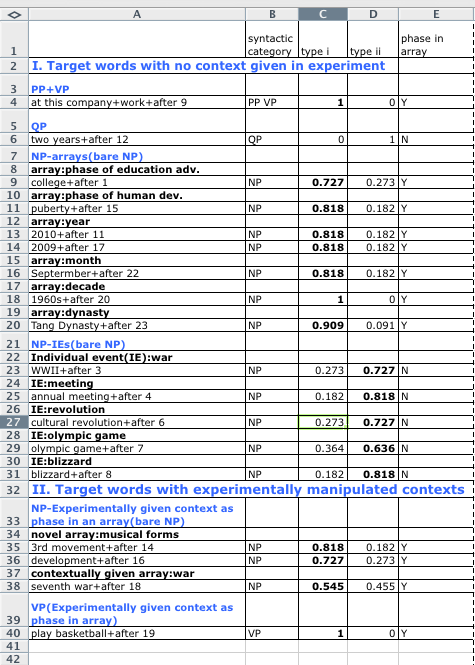
Hypothesis 1 did not work with the data. From the above chart we can see that the interpretation of bare NPs+yihou is not categorical, but gradient. This is also seen in the table on the right above.
Hypothesis 2: bare NPs is interpreted probabilistically from native speaker's statistical learning of the usage frequency of the non-bare NPs+yihou.
Hypothesis 2 captures our initial analysis of the actual results from the experiment. We will do some statistical modeling to include the factors that play a role in the interpretation of temporal meaning of 'yihou'. This model will be able to predict some quantitative results. We will check whether these results borne out in our data.
Assume that p1 is the probability that a bare NP+yihou will be interpreted as a phase in an array; P1 is the probability that a phase will be interpreted as i; p2 is the probability that a bare NP+yihou will be interpreted as a individual event; P2 is the probability that an individual event will be interpreted as ii. Overall, we observe:
P1>>(1-P2)
P2>>(1-P1)
In fact, we predicted that P1 and P2 are pretty close to 1. However, the p1 and p2 part are somewhat problematic: they are correlated with the usage frequency where a particular NP is interpreted as a phase or an IE, f1 and f2 (the distinction between PROBABILITY and OBSERVED FREQUENCY).
Let's assume that if a word is non-categorical, it will be either interpreted as a phase or an IE. Therefore we get f2=1-f1. In this case, if a NP (such as 'war') is frequently interpreted as an IE (such as in WWII), then f2 is quite close to 1, and when the same NP is experimentally manipulated into a mindset where it is a phase in an array, then we can predict that p1 will be somehow lower than it would be if f2 is quite low.
We can predict that in the case of 'war', because f2 is pretty big, therefore, the chance Pi that it will be interpreted as a type i meaning when combined with 'yihou' is much lower than it would be if f2 is pretty low (i.e., the word has no strong existing tendency to be associated with an IE). We can also predict that if f1 is high, then Pi will be higher, i.e., if in the case of a novel array where the NP is not strongly inclined to an IE, Pi is predicted to be higher.
We will develop some more detailed statistical models in the next section, and make some predictions from the model. Then we show that these predictions are generally well borne out by the experiment results.
Hypothesis 2: bare NPs is interpreted probabilistically from native speaker's statistical learning of the usage frequency of the non-bare NPs+yihou.
Hypothesis 2 captures our initial analysis of the actual results from the experiment. We will do some statistical modeling to include the factors that play a role in the interpretation of temporal meaning of 'yihou'. This model will be able to predict some quantitative results. We will check whether these results borne out in our data.
Assume that p1 is the probability that a bare NP+yihou will be interpreted as a phase in an array; P1 is the probability that a phase will be interpreted as i; p2 is the probability that a bare NP+yihou will be interpreted as a individual event; P2 is the probability that an individual event will be interpreted as ii. Overall, we observe:
P1>>(1-P2)
P2>>(1-P1)
In fact, we predicted that P1 and P2 are pretty close to 1. However, the p1 and p2 part are somewhat problematic: they are correlated with the usage frequency where a particular NP is interpreted as a phase or an IE, f1 and f2 (the distinction between PROBABILITY and OBSERVED FREQUENCY).
Let's assume that if a word is non-categorical, it will be either interpreted as a phase or an IE. Therefore we get f2=1-f1. In this case, if a NP (such as 'war') is frequently interpreted as an IE (such as in WWII), then f2 is quite close to 1, and when the same NP is experimentally manipulated into a mindset where it is a phase in an array, then we can predict that p1 will be somehow lower than it would be if f2 is quite low.
We can predict that in the case of 'war', because f2 is pretty big, therefore, the chance Pi that it will be interpreted as a type i meaning when combined with 'yihou' is much lower than it would be if f2 is pretty low (i.e., the word has no strong existing tendency to be associated with an IE). We can also predict that if f1 is high, then Pi will be higher, i.e., if in the case of a novel array where the NP is not strongly inclined to an IE, Pi is predicted to be higher.
We will develop some more detailed statistical models in the next section, and make some predictions from the model. Then we show that these predictions are generally well borne out by the experiment results.
[Statistical modeling and predictions]
According to the rough ideas above, we know what our model will need to do. Basically it will predict different behaviors of the words across different frequency bins.
Assume that a bare NP+yihou has the probability p1 to be interpreted as a phase. (a duration NP is unambiguous and we will not consider them part of the option). Therefore the probability it will be interpreted as a IE is 1-p1. We will focus on how p1 is decided and vary across words. Here we propose that
p1=Pbase+Pcon
where Pbase is the base probability that an NP will be interpreted as a phase in an array. Pbase is determined based on word meaning that is available to the language user: if a word clearly belongs to part of an array that one can easily identify, it is a phase (in this sense, a word like college, WWII, puberty and 2010 will have a Pbase=1). Pcon is the probability that it can be interpreted as a phase in an array given the right context. For example, in the experiment, context are manipulated so that the subjects are given the mindset that the '7th war' is part of an array of wars. If no context is given, this will be set to 0.
Next we will consider the observed frequency (across the entire language) that a particular NP is interpreted as a phase. This frequency f1 should be fixed given the scope of a corpus under investigation (even though strictly speaking it varies across speaker in their own production and in their environmental input. here the variation can be disregarded).
As discussed above, we will have to take into account the effect of f1 to predict the probability of a word being a phase.
Now we've taken care of the p1. Next step is to address the probability that a phase is interpreted as either type i or type ii, P( i | Phase) . Given our data, this probability is certainly not a 50/50. We will expect that it should be quite close to 1 for type i. Here, we derive an estimate of the value of this frequency Fp by computing the total frequency across arrays where a phase in an array is interpreted as type i. The IE will have an opposite effect.
To summarize, in order to compute the probability Pi that a given bare NP+yihou will be interpreted as type i temporal meaning, we have:
Pi=(Pbase+Pcon+C) * f1 * P ( i | Phase)=(Pbase+Pcon+C) * f1 * Fp
where C is a normalizing constant (very small) in the case where Pbase and Pcon are both 0 (such as in the case of 'annual meeting').
From this, we can predict how different words will manifest different frequency of being type i based on these parameters. For example, we expect to find difference between a novel array (e.g., presentation, development, and recapitulation in a sonata form) and a contextual array that is otherwise strongly interpreted as IE and type ii (such as wars). For novel arrays, existing observed frequencies for a phase NP to be of type i or ii are both low, therefore we give fnovel1=0.5 (there is a 50% chance it will be interpreted as a phase), whereas fwar1<<0.5. However the f1 for 'college' as we have observed is pretty high in this temporal context 'college+yihou', therefore having a value quite close to 1. We then expect the novel phase to do better than war phase, but still not as well as college phase. War phase is in in turn than war IE. We predict that:
Pcollege>Pnovel>Pwar-phase>Pwar-ie
Where P is the probability that this NP is interpreted as type i temporal meaning.
These four results are given in numbering 1, 16, 18 and 3 in the chart above (blue line). We can see that the results match our prediction pretty well:
F1>=F16>F8>F3
In fact, the fact that F1=F16 in this particular result shows that the frequency for 'college' being interpreted as type i is not as strong as we have projected. In other words, college+after are more often than we think to be interpreted as after the end of college. This is somehow unexpected but observed in our current results. Also, we do observe that F14>F16, confirming our prediction, since the 'third movement' should be more frequent and less of a jargon than a phase in the sonata form.
Alternatively, we can use year such as 2010 as an example of high frequency type i phase word: after all the year array appear quite frequently in speech in general. A instance of year is given in number 17, where we can clearly observe:
F17>F16>F8>F3.
Two things are curious about the results above. First, the month array (september, number 22) is not is quite high as year array. This could be due to sample size. But we must note that the frequency of a word is not equal to the frequency of the word being interpreted as a phase or type i in temporal meaning. Therefore, even though year and month words are both frequent in natural language, they do not have the same frequency of being type i meaning (at least in the current study).
The second curious fact about the results is that among the three NPs that got a 100% rating of type i meaning, two of them are not NPs: they are [PP+V] and a VP that is contextually manipulated into an array meaning, which otherwise would be plainly an IE type VP of type ii meaning. More work maybe carried out as to whether these types of syntactic constructions are really more robust than NPs. One explanation for this is that both of these constructions do not have contextual structural variation comparing to the bare NPs. As we observed in the corpus, bare NPs commonly co-occur with other structural non-NP items (such as 'enter+college+after', or a preposition before the NP), therefore making the interpretation about bare NPs less robust and more varied comparing to VPs. VPs, when manipulated in the right array context, cannot have other structural items closely added to them, therefore more robust in their meaning type.
Assume that a bare NP+yihou has the probability p1 to be interpreted as a phase. (a duration NP is unambiguous and we will not consider them part of the option). Therefore the probability it will be interpreted as a IE is 1-p1. We will focus on how p1 is decided and vary across words. Here we propose that
p1=Pbase+Pcon
where Pbase is the base probability that an NP will be interpreted as a phase in an array. Pbase is determined based on word meaning that is available to the language user: if a word clearly belongs to part of an array that one can easily identify, it is a phase (in this sense, a word like college, WWII, puberty and 2010 will have a Pbase=1). Pcon is the probability that it can be interpreted as a phase in an array given the right context. For example, in the experiment, context are manipulated so that the subjects are given the mindset that the '7th war' is part of an array of wars. If no context is given, this will be set to 0.
Next we will consider the observed frequency (across the entire language) that a particular NP is interpreted as a phase. This frequency f1 should be fixed given the scope of a corpus under investigation (even though strictly speaking it varies across speaker in their own production and in their environmental input. here the variation can be disregarded).
As discussed above, we will have to take into account the effect of f1 to predict the probability of a word being a phase.
Now we've taken care of the p1. Next step is to address the probability that a phase is interpreted as either type i or type ii, P( i | Phase) . Given our data, this probability is certainly not a 50/50. We will expect that it should be quite close to 1 for type i. Here, we derive an estimate of the value of this frequency Fp by computing the total frequency across arrays where a phase in an array is interpreted as type i. The IE will have an opposite effect.
To summarize, in order to compute the probability Pi that a given bare NP+yihou will be interpreted as type i temporal meaning, we have:
Pi=(Pbase+Pcon+C) * f1 * P ( i | Phase)=(Pbase+Pcon+C) * f1 * Fp
where C is a normalizing constant (very small) in the case where Pbase and Pcon are both 0 (such as in the case of 'annual meeting').
From this, we can predict how different words will manifest different frequency of being type i based on these parameters. For example, we expect to find difference between a novel array (e.g., presentation, development, and recapitulation in a sonata form) and a contextual array that is otherwise strongly interpreted as IE and type ii (such as wars). For novel arrays, existing observed frequencies for a phase NP to be of type i or ii are both low, therefore we give fnovel1=0.5 (there is a 50% chance it will be interpreted as a phase), whereas fwar1<<0.5. However the f1 for 'college' as we have observed is pretty high in this temporal context 'college+yihou', therefore having a value quite close to 1. We then expect the novel phase to do better than war phase, but still not as well as college phase. War phase is in in turn than war IE. We predict that:
Pcollege>Pnovel>Pwar-phase>Pwar-ie
Where P is the probability that this NP is interpreted as type i temporal meaning.
These four results are given in numbering 1, 16, 18 and 3 in the chart above (blue line). We can see that the results match our prediction pretty well:
F1>=F16>F8>F3
In fact, the fact that F1=F16 in this particular result shows that the frequency for 'college' being interpreted as type i is not as strong as we have projected. In other words, college+after are more often than we think to be interpreted as after the end of college. This is somehow unexpected but observed in our current results. Also, we do observe that F14>F16, confirming our prediction, since the 'third movement' should be more frequent and less of a jargon than a phase in the sonata form.
Alternatively, we can use year such as 2010 as an example of high frequency type i phase word: after all the year array appear quite frequently in speech in general. A instance of year is given in number 17, where we can clearly observe:
F17>F16>F8>F3.
Two things are curious about the results above. First, the month array (september, number 22) is not is quite high as year array. This could be due to sample size. But we must note that the frequency of a word is not equal to the frequency of the word being interpreted as a phase or type i in temporal meaning. Therefore, even though year and month words are both frequent in natural language, they do not have the same frequency of being type i meaning (at least in the current study).
The second curious fact about the results is that among the three NPs that got a 100% rating of type i meaning, two of them are not NPs: they are [PP+V] and a VP that is contextually manipulated into an array meaning, which otherwise would be plainly an IE type VP of type ii meaning. More work maybe carried out as to whether these types of syntactic constructions are really more robust than NPs. One explanation for this is that both of these constructions do not have contextual structural variation comparing to the bare NPs. As we observed in the corpus, bare NPs commonly co-occur with other structural non-NP items (such as 'enter+college+after', or a preposition before the NP), therefore making the interpretation about bare NPs less robust and more varied comparing to VPs. VPs, when manipulated in the right array context, cannot have other structural items closely added to them, therefore more robust in their meaning type.
data processing snapshots
#comparing means of type 1 rating percentage in R
> phase<-c(0.727,0.818,0.818,0.818,0.818,1,0.909,0.818,0.727,0.545)
> nonphase<-c(0.273,0.182,0.273,0.364,0.182)
> t.test(phase,nonphase)
Welch Two Sample t-test
data: phase and nonphase
t = 10.6992, df = 11.917, p-value = 1.829e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.4339294 0.6560706
sample estimates:
mean of x mean of y
0.7998 0.2548
> phase<-c(0.727,0.818,0.818,0.818,0.818,1,0.909,0.818,0.727,0.545)
> nonphase<-c(0.273,0.182,0.273,0.364,0.182)
> t.test(phase,nonphase)
Welch Two Sample t-test
data: phase and nonphase
t = 10.6992, df = 11.917, p-value = 1.829e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.4339294 0.6560706
sample estimates:
mean of x mean of y
0.7998 0.2548